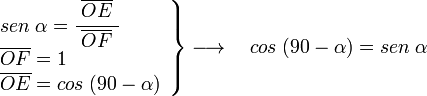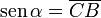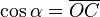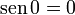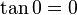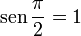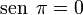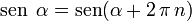ANGULOS DE INCLINACION Y PENDIENTES

ÁNGULO DE INCLINACIÓN

La inclinación de una recta cualquiera (que no sea paralela al eje X) es el ángulo menor que la recta forma con la dirección positiva del eje X, y se mide desde el eje X hacia la recta, en el sentido contrario a las manecillas del reloj.

El valor de los catetos del triángulo rectángulo formado se determina por diferencia de segmento como en el tema anterior.

F.T en el plano carteciano

Funciones trigonométricas

Representación gráfica

 

CALCULO DE ALGUNOS CASOS

Para 90-α

Si a partir del eje vertical OB trazamos la recta r a un ángulo α en el sentido horario, la recta r forma con el eje x un ángulo 90-α, el valor de las funciones trigonométricas de este ángulo conocidas las de α serán:

El triángulo OEF rectángulo en E, siendo el ángulo en F α, por lo tanto:

en el mismo triángulo OEF, tenemos que:

viendo el triángulo OAG, rectángulo en A, siendo el ángulo en G igual a α, podemos ver:

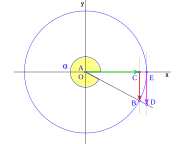
Sentido de las funciones trigonométricas

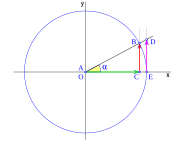
Dados los ejes de coordenadas cartesianas xy, de centro O, y una circunferencia goniométrica (circunferencia de radio la unidad) con centro en O; el punto de corte de la circunferencia con el lado positivo de las x, lo señalamos como punto E.
Nótese que el punto A es el vértice del triángulo, y O es el centro de coordenada del sistema de referencia:

a todos los efectos.
La recta r, que pasa por O y forma un ángulo sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
Por semejanza de triángulos:

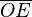Los puntos E y B están en la circunferencia de centro O, por eso la distancia y son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:

tenemos:

La tangente es la relación del seno entre el coseno, según la definición ya expuesta.

Primer cuadrante

 

Para ver la evolución de las funciones trigonométricas según aumenta el ángulo, daremos una vuelta completa a la circunferencia, viéndolo por cuadrantes, los segmentos correspondientes a cada función trigonométrica variaran de longitud, siendo esta variación función del ángulo, partiendo en el primer cuadrante de un ángulo cero.
Partiendo de esta representación geométrica de las funciones trigonométricas, podemos ver las variaciones de las funciones a medida que aumenta el ángulo .
Para 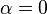, tenemos que B, D, y C coinciden en E, por tanto:

Si aumentamos progresivamente el valor de , las distancias y aumentarán progresivamente, mientras que 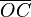disminuirá.
Percatarse que el punto B es de la circunferencia y cuando el ángulo aumenta se desplaza sobre ella.
El punto E es la intersección de la circunferencia con el eje x y no varia de posición.
Los segmentos: 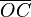y están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por E, en el momento en el que el ángulo rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia será infinita.
El punto C coincide con A y el coseno vale cero. El punto B esta en el eje y en el punto más alto de la circunferencia y el seno toma su mayor valor: uno.
Para un ángulo recto las funciones toman los valores:

Segundo cuadrante

 

 

Cuando el ángulo supera el ángulo recto, el valor del seno empieza a disminuir según el segmento , el coseno aumenta según el segmento 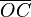, pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
La tangente para un ángulo inferior a rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por E en el punto D real, en el lado negativo de las y, la tangente por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo aumenta progresivamente hasta los 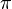rad.
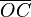Resumiendo: en el segundo cuadrante el seno de , , disminuye progresivamente su valor desde 1, que toma para rad, hasta que valga 0, para rad, el coseno,, toma valor negativo y su valor varia desde 0 para rad, hasta –1, para rad.
La tangente conserva la relación:

incluyendo el signo de estos valores.
Para un ángulo llano tenemos que el punto D esta en E, y B y C coinciden en el eje de las x en el lado opuesto de E, con lo que tenemos:

Tercer cuadrante

 

 

En el tercer cuadrante, comprendido entre los valores del ángulo rad a 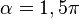rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para 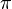rad:

Cuando el ángulo aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
A medida que el ángulo crece el punto C se acerca a O, y el segmento 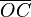, el coseno, se hace más pequeño en el lado negativo de las x.
El punto B, intersección de la circunferencia y la vertical que pasa por C, se aleja del eje de las x, en el sentido negativo de las y, el seno, .
Y el punto D, intersección de la prolongación de la recta r y la vertical que pasa por E, se aleja del eje las x en el sentido positivo de las y, con lo que la tangente, , aumenta igual que en el primer cuadrante
Cuando el ángulo alcance rad, el punto C coincide con O y el coseno valdrá cero, el segmento será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
El seno el coseno y la tangente siguen conservando la misma relación:

que se cumple tanto en valor como en signo, nótese que cuando el coseno vale cero, la tangente se hace infinito.

 Cuarto cuadrante

 

 

En el cuarto cuadrante, que comprende los valores del ángulo entre rad y rad, las variables trigonométricas varían desde los valores que toman para rad:

hasta los que toman para rad pasando al primer cuadrante, completando una rotación:

como puede verse a medida que el ángulo aumenta, aumenta el coseno 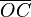en el lado positivo de las x, el seno disminuye en el lado negativo de las y, y la tangente también disminuye en el lado negativo de las y.
Cuando , vale ó al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.
Dado el carácter rotativo de las funciones trigonométricas, se puede afirmar en todos los casos:

Que cualquier función trigonométrica toma el mismo valor si se incrementa el ángulo un número entero de rotaciones completas.