LOS TRES CERITOS
Eranse una vez tres ceritos que vivían en un cuerpo K. Uno era muy listo, otro muy vago, y otro muy confiado.
Un buen día llegó a visitarles su amigo el uno. En muchos cuerpos como éste, era costumbre que el uno hiciera estas visitas cada cierto tiempo característico (la característica de un cuerpo es el menor entero n tal que 1+...+1(n veces)=0), que dependía del cuerpo donde vivían. Sin embargo, ese día, su amigo les trajo malas noticias.
-"Lo siento amigos míos, pero tendréis que marcharos. El congreso acaba de aprobar una ley conocida como `Teorema de unicidad de elementos neutros para la suma.' que prohibe la estancia en el cuerpo de más de un cero."
-"¡Oh, vaya!, dos de nosotros tendrán que irse.", dijo uno de los ceritos.
-"Lo siento, pero el puesto ya está cogido por un cero con enchufe. Dicen que es primo del famoso Cero de Hilbert. Temo que tendréis que iros los tres."
Apenados, los ceritos cogieron sus pertenencias, y se fueron mucho más allá de las extensiones finitas, a un espacio normado propiedad de un multimillonario llamado Hausdorff, amigo de los ceritos, el cual les dejó vivir allí.
Como había mucho terreno libre por habitante, debido a que la topología empleada en la construcción del espacio era
muy fina, decidieron construirse una casita para cada uno.
-"Yo me haré una casita con hiperplanos." dijo el cerito más confiado. Dicen que este cerito era tan confiado, que cuando iba al médico a hacerse un análisis matemático, siempre se los hacía sin ningun tipo de rigor.
-"Yo me construiré una casa con matrices." dijo el cerito más vago. Malas lenguas contaban que era tan vago, que en la fábrica de ecuaciones donde trabajaba, sólo producía ecuaciones con solución trivial.
-"Pero deberíais haceros casas más fuertes, pues sé que por aquí ronda una esfera descentrada muy feroz, que os comerá cuando tenga la oportunidad.", dijo el cerito sabio. Cuentan que este cerito era tan sabio que incluso ¡aprendió a dividir números! (segun la definición de divisibilidad, el cero no puede dividir a ningun número).
-"¡Bah, no tenemos miedo de esa esfera, nuestras casitas nos protegerán!."
-"Haced lo que queráis, pero yo me haré una casa fuerte, compacta, y por lo tanto cerrada y acotada.", y dicho esto, se marchó.
Al cabo de un tiempo, cada cerito había terminado su casita. El cerito confiado tenía su casita hecha de hiperplanos y el cerito vago su casita compuesta enteramente de matrices.
Al cerito sabio le costó mucho trabajo hacer su casa, pues primero tuvo que comprar un 3-cubo compacto y empezar a parametrizar la casa. Cuando acabó, se dió cuenta de que el tejado tenía algunas discontinuidades evitables que producirían goteras cuando lloviera, así que tuvo que comprar unos cuantos abiertos para recubrir los agujeros por continuidad.
Una vez terminada la casa, comenzó a construirle una cota alrededor (como su casa era compacta, sabía que podría construir una), pero como había tenido la precaución de hacer su casa diferenciable pudo localizar fácilmente los puntos más alejados y a partir de ahí construir la cota.
Como véis al cerito sabio le fueron muy útiles sus conocimientos sobre derivadas, que aprendió de sus múltiples peregrinaciones por la Ruta Jacobiana.
Pasó el tiempo, y la esfera se percató de ellos.
-"Parece que tenemos aquí comida deliciosa. Me alegro, empezaba a estar harto de alimentarme de restos de divisiones euclídeas."
Y dicho esto, la malvada esfera fue directa a casa del cerito confiado (como estaba descentrada, la malvada esfera podía moverse por donde quisiera). (Dado que todos los puntos deben distar siempre lo mismo del centro).
No tardó mucho en encontrar al cerito confiado, pues mirara por donde mirara, siempre veía parte de su casa, (una recta y un hiperplano proyectivos siempre se cortan, en este caso, la recta es la mirada de la esfera y el hiperplano el material de que está hecha la casa del cerito confiado) así que fue hacia allí.
-"¡Cerito, si no abres la puerta soplaré, soplaré y la casa proyectaré!.", amenazó la esfera.
-"No te tengo miedo, esfera cruel, mi casa es toda de hiperplanos dobles y aguantará.", respondió el cerito.
Pero lo que no sabía el cerito era que la esfera había perdido un punto en un accidente con un equipo estereográfico (la proyección estereográfica parametriza toda la esfera menos un punto).
Se hinchó por el punto que le faltaba, y sopló tan fuerte, que dualizó la casa del cerito convirtiendo los hiperplanos de ésta en un montoncito de puntos insignificantes. El cerito, asustado, salió corriendo por una sucesión que convergía directamente a casa del cerito vago.
La malvada esfera salió corriendo detras del cerito, pero nuestro amigo atajó por una subsucesión que le llevó a su destino más rápidamente. Por suerte, la esfera prefirió no adentrarse en la subsucesión por miedo a perderse (aquí se hace patente la ignorancia de la esfera de no conocer el Teorema Fundamental del Límite: En una sucesión que converge, cualquier subsucesión converge al mismo sitio), con lo que el cerito llegó con tiempo de avisar al cerito vago y de resguardarse en la casita hecha de matrices.
Al cabo de un rato llegó la esfera. Gritó:
-"¡Jo, jo, da igual dos ceros que n ceros o uno solo, no podeis nada contra mí, salid inmediatamente o soplaré, soplaré y la casa reduciré!."
-"No quiero salir, esfera, mi casa es totalmente hermítica y aguantará!.", respondió el cerito.
Entonces la esfera sopló y sopló tan fuerte que redujo todas las matrices de la casa por columnas (si la esfera hubiera soplado hacia arriba o abajo, hubiera reducido las matrices por filas), convirtiendo la casa en un esqueleto compuesto de incógnitas (el cerito vago había usado matrices de ecuaciones sin molestarse siquiera en resolverlas). Por si fuera poco los dos ceritos hubieran salido volando de no ser porque se agarraron a un pivote de una matriz que todavía quedaba en pie.
Pero ¿por qué era tan mala la esfera?. Según se cuenta, la esfera estuvo trabajando en una banda criminal llamada La Banda de Moebius, de ahí su carácter retorcido. Pero volvamos a nuestro cuento.
Despavoridos, los ceritos salieron corriendo a casa del cerito sabio. Lo encontraron montado en una tractriz, plantando grafos en su huerto. Corrían tanto que saltaron la cota de la casa de un salto.
-"¡Socorro, socorro, ayúdanos cerito sabio, la esfera quiere devorarnos!."
-"No os preocupéis, entrad en mi casa, veréis cómo la esfera no puede hacernos daño.", dijo el cerito sabio. Y dicho esto, se metieron en la casa.
Al cabo de un rato llegó la esfera malvada. No le costó trabajo encontrar el camino porque uno de los ceritos pisó un punto de tinta de modo que sólo tuvo que seguir la cicloide (si una circunferencia rueda sobre una recta, la curva que describe cualquiera de sus puntos se llama cicloide; no olvidemos que los ceritos son redondos.) que iban dejando tras ellos.
Una vez que llegó, gritó con todas sus fuerzas:
-"¡Por fin os tengo a los tres juntos, salid o soplaré, soplaré y la casa despejaré!.".
-"Nunca", dijo el cerito sabio, "mi casa es fuerte y aguantará".
Entonces la malvada esfera sopló y sopló, pero como la casa era compacta, sólo llegaron a ella un número finito de soplidos, lo cual no llegó a afectarle mucho. La esfera, obstinada, sopló y sopló con todas sus fuerzas, pero el cerito sabio había tenido la precaución de hacerse una casa con superficie Gaussiana, con lo cual todos los soplidos de la esfera se repelieron mutuamente.
La esfera quedó exhausta, y el cerito sabio aprovechó ese momento para dejar caer sobre ella un pesado atlas de 6 tomos que recubrieron totalmente a la esfera dejando a ésta aprisionada.
Entonces los ceritos agarraron a la esfera por una de sus geodésicas y tirando, tirando, consiguieron deshilacharla y convertirla en una curva, y hecho esto la llevaron a R^2 donde ahora podría llevar una vida con parámetro natural.
Hecho esto, los ceritos agradecieron al cerito sabio su ayuda y prometieron ser más trabajadores y menos confiados.


 El concepto y la fórmula general del interés compuesto es una potente herramienta en el análisis y evaluación financiera de los movimientos de dinero.
El concepto y la fórmula general del interés compuesto es una potente herramienta en el análisis y evaluación financiera de los movimientos de dinero. 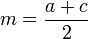

![h = \frac {\sqrt{4(a-c)^2d^2 -[d^2+(a-c)^2-b^2]^2}}{2(a-c)}](http://upload.wikimedia.org/math/c/4/1/c414edd7800d557f9ad66f642f5e81c4.png)