Sin embargo, para calcular el área de superficies curvas se requiere introducir métodos de geometría diferencial.
Para poder definir el área de una superficie en general –que es un concepto métrico–, se tiene que haber definido un tensor métrico sobre la superficie en cuestión: cuando la superficie está dentro de un espacio euclídeo, la superficie hereda una estructura métrica natural inducida por la métrica euclídea.
Área de figuras planasÁrea de un triángulo
El área de un triángulo se calcula mediante la siguiente fórmula:
donde b es la base del triángulo y h es la altura correspondiente a la base. (se puede considerar cualquier lado como base)

Si el triángulo es rectángulo, la altura coincide con uno de los catetos, y la fórmula quedaría de la siguiente forma:

donde a y b son los catetos.
Si lo que conocemos es la longitud de sus lados aplicamos la fórmula de Herón.

donde a, b , c son los valores de las longitudes de sus lados s = ½ (a + b + c) es el semiperimetro del triángulo.
Si el triángulo es equilátero, de lado a, su área está dada por
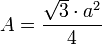
Área es la extensión o
Área de un cuadrilátero
El rectángulo es un paralelogramo cuyos ángulos son todos de 90º; el área sería la multiplicación de dos de sus lados contiguos a y b:

El rombo, cuyos 4 lados son iguales, tiene su área dada por el semiproducto de sus dos diagonales:

El cuadrado es el polígono regular de cuatro lados, es a la vez un rectángulo y un rombo, por lo que su área puede ser calculada de la misma manera que la de estos dos. En particular, dado que sus lados son iguales, se usa la fórmula:

Los paralelogramos en general tienen su área dada por el producto uno de sus lados y su altura respectiva:

El trapecio (que tiene dos lados paralelos entre sí y dos lados no paralelos) cuya área viene dada por la media aritmética de sus lados paralelos multiplicado por la distancia entre ellos (altura)

Además de las fórmulas para calcular áreas de las figuras geométricas planas más comunes, debes tener en cuenta las siguientes áreas circulares.
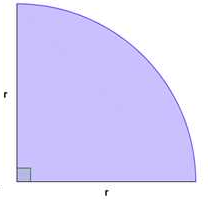 | CUADRANTE 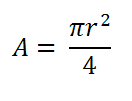 |
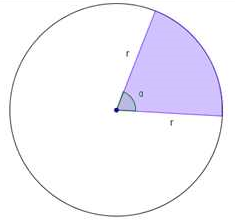 | SECTOR CIRCULAR 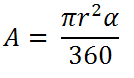 |
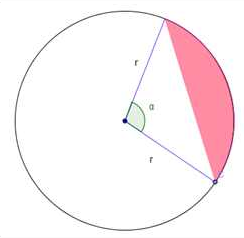 | SEGMENTO CIRCULAR 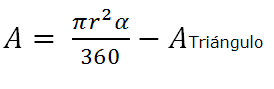 |
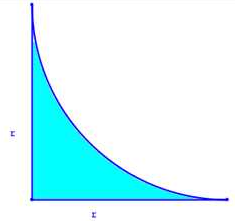 | EMBECADURA 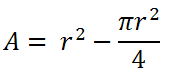 |
No hay comentarios:
Publicar un comentario